栈
- 逻辑结构:线性表
- 存储结构:顺序存储\链式存储
- 基本运算:
- 初始化
- 判断栈空
- 判断栈满
- 入栈
- 出栈
- 取栈顶元素
注意:栈也是线性表,其特殊性在于有特殊的运算规则。即:栈结构只能在一端进行操作,该操作端称为栈顶,另一端称为栈底。按照“后进先出”(Last In First Out,LIFO)原则处理数据节点。
1. 顺序栈
1
2
3
4
5
6
| typedef struct stack
{
int *base; // 基地址
int *top; // 栈顶指针
int stackSize; // 栈容量
}*Stack;
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| Stack Init_Stack(Stack S) // 栈的初始化
{
S=(Stack)malloc(sizeof(Stack));
if(!S)
exit(0);
S->base = (int*)malloc(STACK_INIT_SIZE*sizeof(DATATYPE));
if(!S->base)
exit(0);
S->top = S->base;
S->stackSize = STACK_INIT_SIZE;
return S;
}
|
判断栈空
栈底等于栈顶即为空。1
2
3
4
5
6
7
8
9
| int IsEmpty(Stack S)
{
if (S->top == S->base){
return 1;
}
else{
return 0;
}
}
|
判断栈满
栈顶减栈底等于栈容量即为栈满。1
2
3
4
5
6
7
8
9
10
| int IsFull(Stack S)
{
if (S->top - S->base == S->stackSize) {
return 1;
}
else{
return 0;
}
}
|
顺序栈的入栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| void Push(Stack S, DATATYPE e) // 数据压进栈
{
assert(S);
if (IsFull(S))
{
S->base = (int*)malloc((STACK_INIT_SIZE+STACK_INCREMENT)*sizeof(DATATYPE));
if (!S->base)
exit(0); // 存储分配失败
S->top = S->base + S->stackSize;
S->stackSize += STACK_INCREMENT;
}
*S->top++ = e;
}
|
1
2
3
4
5
6
7
8
9
10
| DATATYPE Pop(Stack S)
{
assert(S);
if (S->top == S->base)
return 0;
else
{
return *--S->top; // *--S->top就是*(--S->top)
}
}
|
取栈顶元素
1
2
3
4
5
6
7
8
9
10
11
| // 访问栈顶
DATATYPE GetTop(Stack S)
{
assert(S);
if (S->top == S->base)
return 0;
else
{
return *(S->top-1);
}
}
|
注意:取栈顶元素与出栈的区别:
*出栈:数据从栈中移出,
取栈顶:只是访问了一下栈顶,数据还在栈中。*
顺序栈的销毁
1
2
3
4
| void DestroyStack(Stack S) {
free(S->base);
free(S);
}
|
总的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
| #include <stdio.h>
#include <stdlib.h>
#include <assert.h> // 断言函数
#define STACK_INIT_SIZE 100 // 栈容量
#define STACK_INCREMENT 10 // 栈增量
typedef int DATATYPE;
typedef struct stack
{
int *base; // 基地址
int *top; // 栈顶指针
int stackSize; // 栈容量
}*Stack;
// 栈的初始化
Stack Init_Stack(Stack S)
{
S=(Stack)malloc(sizeof(Stack));
if(!S)
exit(0);
S->base = (int*)malloc(STACK_INIT_SIZE*sizeof(DATATYPE));
if(!S->base)
exit(0);
S->top = S->base;
S->stackSize = STACK_INIT_SIZE;
return S;
}
// 判栈空
int IsEmpty(Stack S)
{
if (S->top == S->base){
return 1;
}
else{
return 0;
}
}
// 判栈满
int IsFull(Stack S)
{
if (S->top - S->base == S->stackSize) {
return 1;
}
else{
return 0;
}
}
// 操作数压栈
void Push(Stack S, DATATYPE e)
{
assert(S);
if (IsFull(S))
{
S->base = (int*)malloc((STACK_INIT_SIZE+STACK_INCREMENT)*sizeof(DATATYPE));
if (!S->base)
exit(0); // 存储分配失败
S->top = S->base + S->stackSize;
S->stackSize += STACK_INCREMENT;
}
*S->top++ = e;
}
// 操作数弹栈
DATATYPE Pop(Stack S)
{
assert(S);
if (S->top == S->base)
return 0; // 空栈弹出0保证部分负数的正确运算
else
{
return *--S->top; // *--S->top就是*(--S->top)
}
}
// 访问栈顶
DATATYPE GetTop(Stack S)
{
assert(S);
if (S->top == S->base)
return 0;
else
{
return *(S->top-1);
}
}
// 栈的销毁
void DestroyStack(Stack S) {
free(S->base);
free(S);
}
int main()
{
Stack OPND=NULL;
OPND = Init_Stack(OPND); // 创建操作数栈
int i;
for (i=0; i<5; i++)
{
Push(OPND,i);
}
for (i=0; i<5; i++)
{
printf("此时的栈顶为:%d\n",GetTop(OPND));
printf("将%d出栈\n",Pop(OPND));
}
DestroyStack(OPND);
return 0;
}
|
1
2
3
4
5
6
7
8
9
10
11
| typedef struct node //定义节点
{
DATATYPE data;
struct node * next;
} StackNode;
typedef struct //定义一个链栈
{
StackNode * top; //总指向栈顶
int count; //计数器 记录链栈的元素个数
}Stack,*LinkStack;
|
1
2
3
4
5
| void init(LinkStack s)
{
s->top=NULL; //该指针箭头指向为空
s->count=0; //初始化时长度为零
}
|
1
2
3
4
| int IsEmpty(LinkStack s)
{
return (s->top==NULL? TRUE:FALSE);
}
|
回到目录
1
2
3
4
5
6
7
8
9
10
11
12
13
| void push(LinkStack s,DATATYPE a)
{
StackNode * p=(StackNode *)malloc(sizeof(StackNode));
if(NULL==p) //申请不成功
exit(1);
else
{
p->data=a;
p->next=s->top; //将新节点的指针域指向原栈顶节点
s->top=p; //栈顶指针指向新节点
s->count++;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| DATATYPE pop(LinkStack s)
{
DATATYPE a;
if( IsEmpty(s))
return FALSE;
else
{
a =s->top->data; //将即将弹出的数据存在a中。不存也不影响出栈操作
s->top=s->top->next;
s->count--;
free(s->top);
return a;
}
}
|
1
2
3
4
5
6
7
8
9
| DATATYPE GetTop(LinkStack S)
{
if(IsEmpty(S))
return FALSE;
else
{
return S->top->data;
}
}
|
回到目录
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
| # include<stdio.h>
# include<stdlib.h>
# define FALSE 0
# define TRUE 1
typedef int DATATYPE;
typedef struct node //定义节点
{
DATATYPE data;
struct node * next;
} StackNode;
typedef struct //定义一个链栈
{
StackNode * top; //总指向栈顶
int count; //计数器 记录链栈的元素个数
}Stack,*LinkStack;
void init(LinkStack s); //初始化
int IsEmpty(LinkStack s); //判断是否为空(链栈一般不会为满)
void push(LinkStack s,DATATYPE a); //入栈
DATATYPE pop(LinkStack s); //出栈
DATATYPE GetTop(LinkStack S); //取栈顶元素
int length(LinkStack s); //取链栈长度
void init(LinkStack s)
{
s->top=NULL; //该指针箭头指向为空
s->count=0; //初始化时长度为零
}
int IsEmpty(LinkStack s)
{
return (s->top==NULL? TRUE:FALSE);
}
void push(LinkStack s,DATATYPE a)
{
StackNode * p=(StackNode *)malloc(sizeof(StackNode));
if(NULL==p) //申请不成功
exit(1);
else
{
p->data=a;
p->next=s->top; //将新节点的指针域指向原栈顶节点
s->top=p; //栈顶指针指向新节点
s->count++;
}
}
DATATYPE pop(LinkStack s)
{
DATATYPE a;
if( IsEmpty(s))
return FALSE;
else
{
a =s->top->data; //将即将弹出的数据存在a中。不存也不影响出栈操作
s->top=s->top->next;
s->count--;
free(s->top);
return a;
}
}
DATATYPE GetTop(LinkStack S)
{
if(IsEmpty(S))
return FALSE;
else
{
return S->top->data;
}
}
int length(LinkStack s)
{
return s->count;
}
int main(void)
{
Stack S;
init(&S); // 创建操作数栈
int i;
for (i=0; i<5; i++)
{
push(&S,i);
}
printf("链栈长度为:%d\n",length(&S));
while(!IsEmpty(&S))
{
printf("此时的栈顶为:%d\n",GetTop(&S));
printf("将%d出栈\n",pop(&S));
}
return 0;
}
|
运行结果
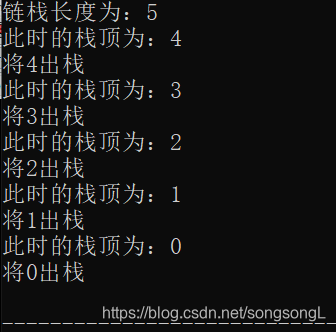
注意:顺序栈的栈顶指向的是即将入栈的位置,没有指着任何数据,所以栈顶减栈底可以判断是否为空或满。而链栈的指针指向的是栈顶的数据,所以s->top==NULL就可以判断是否为空。别搞混了。
回到目录

