songsong的垃圾堆

收废铜烂铁~

0%

二叉树

发表于 更新于 阅读： Valine：
本文字数： 2.9k 阅读时长 ≈ 11 分钟

@[TOC]

1.树结构

  • 在一个树结构中，有且仅有一个结点没有直接前驱，这个结点就是树的根结点。

  • 除根结点外，其余每个结点有且仅有一个直接前驱。

  • 每个结点可以有任意多个直接后继。

    2.树的基本概念

  • 结点（Node）：树中的独立单元。如下图中的A-M。

  • 结点的度（Degree）：结点的子树个数。如下图A的度为3，E的度为2等。

  • 树的度：树内各结点度的最大值。下图树的度为3。

  • 叶子结点（Leaf）：度为0的结点。下图中K、L、F、G、M、I、J都是树的叶子。

  • 父结点（Parent）：有子树的结点是其子树的根节点的父结点。

  • 孩子结点（Child）：结点的子树的根称为该节点的孩子。如下图B的父节点是A，B的孩子有E、F。

  • 兄弟结点（Sibling）：具有同一个父结点的各结点之间互称兄弟。如下图H、I、J互为兄弟。

  • 祖先结点（Ancestor）：沿树根到该结点路径上的所有结点都是这个结点的祖先结点。如下图M的祖先为A、D、H

  • 子孙结点（Descendant）：某一结点的子树中的所有结点是这个结点的子孙。如下图B的子孙为E、K、L、F。

  • 层次（Level）：根为第1层，其他任一结点的层数是其父结点的层数加1。

  • 树的深度（Depth）：树中所有结点中的最大层次是这棵树的深度或高度。下图树的深度为4。

  • 森林（forest）：n（n>0）棵互不相交的树的集合。
    树
    回到目录

    3.二叉树的基本概念

  • 二叉树的定义：

  1. 它是n（n>0）个结点的集合，每个结点最多只能有两个子结点。
  2. 二叉树的子树仍然是二叉树。两个子树分别为左子树和右子树。
  3. 由于子树有左右之分，所以二叉树是有序树。

  • 二叉树的5种基本形态：

    在这里插入图片描述

  • 二叉树的特殊类型：

    • 满二叉树

      深度为k且含有2^k^-1个结点的二叉树。即除叶结点外，每层的结点都有两个子结点。
      在这里插入图片描述

    • 完全二叉树

      除二叉树最后一层外，其他各层的结点数都达到最大个数，且最后一次从左到右要连续存在。
      在这里插入图片描述

注意：满二叉树一定是完全二叉树，但完全二叉树不一定是满二叉树。

回到目录

  • 二叉树的性质：

    • 性质一：在二叉树的第i层上至多有2^(i-1)^个节点(i>=1)。

      证明：利用数学归纳法进行证明
      当i==1时，此时二叉树只有根节点。2^(i-1)^= 1。显然成立，
      假设i>1时，第i层的节点数目为2^(i-1)。
      根据假设，只需证明第i+1层节点数为2^i 即可。
      由于二叉树每个节点最多有两个孩子，故第(i+1)层上的节点数最多是第i层的两倍。
      即：第i+1层上节点数最多为: 2       2^(i-1) = 2 ^ i
      故假设成立，命题得证。*

    • 性质二：深度为k的二叉树至多有2^k^-1个节点。

      证明：二叉树节点数最多时，每层的节点树都必须最多。
      根据性质一，深度为k的二叉树的节点数最多为：公比为2的等比数列前n项和。
      即：2^0^+ 2^1^ +….+2^(k-1)^ = 2 ^ k^ -1

    • 性质三：对任何一棵二叉树T，如果终端节点数为n0，度为2的节点数为 n2 ，那么 n0= n2 +1。

      证明：从结点角度看结点总数，二叉树结点度数最大为2，
      则 ： n = n0+n1+n2 (等式一)
      从分支（线）角度看结点总数，
      则： n = n1+ 2n2+1(根节点)（等式二）
      可以推出 n0= n2 +1

    • 性质四： 具有n个节点的完全二叉树的高度为至少为log2(n+1)

      证明：高度为k的二叉树最多有2^k^–1个结点。反之，对于包含n个节点的二叉树的高度至少为log2(n+1)。

    • 性质五：如果对一棵有n个节点的完全二叉树的节点按层序编号（从第一层开 始到最下一层，每一层从左到右编号），对任一节点i，有：

      1. 如果i=1 ，则结点为根节点，没有双亲。
        如果i>1，则其父节点是 ⌊i/2⌋ 。
      2. 如果2i > n ，则节点i没有左孩子 ；否则其左孩子节点为2*i。
      3. 如果2i+1>n ，则节点i没有右孩子；否则其右孩子节点为2*1+1。

    回到目录

    4.二叉树的操作

  • 顺序存储

    顺序存储使用一组地址连续的存储单元来存取元素，对于完全二叉树，只要从根起按层序存储即可，依次自上而下，自左而右存取结点元素。
    对于一般二叉树，则需将其与完全二叉树的结点相对照，不存在的结点用 “0”或“#” 等代替。因为由性质5可知，顺序存储只能这样去体现出结点间的逻辑关系。
    由此可见，对于一般二叉树，更适合采取链式存储。

  • 链式存储

    由二叉树的特点，可知一个结点至少包含3个域：**数据域和左、右指针域。**

    • 二叉树定义

      1
      2
      3
      4
      5
      6
      7
      typedef char datatype;

      typedef struct BiTNode{			//二叉树节点 
      	datatype data;
      	struct BiTNode *lchild;
      	struct BiTNode *rchild;
      }BiTNode,*BiTree;

    • 初始化

      将根节点初始化为“A”，可随意。

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      void init(BiTree &T){
      	if((T=new BiTNode)!=NULL){
      		T->data='A';
      		T->lchild=NULL;
      		T->rchild=NULL;
      	}
      	else{
      		cout<<"初始化失败"<<endl;
      		exit(1); 
      	}
      }

    • 创建二叉树

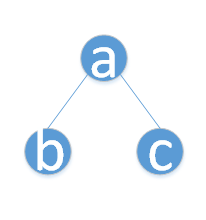
      如：ab##c##，表示这样的二叉树：
      在这里插入图片描述

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      void CreateBiTree(BiTree &T){	//按先序序列创建二叉树 
      	datatype data;
      	cin>>data;
      	if(data=='#') T=NULL;
      	else {
      		T=(BiTree)malloc(sizeof(BiTNode));
      		T->data=data;
      		CreateBiTree(T->lchild);
      		CreateBiTree(T->rchild);
          }
      }

    • 访问结点

      1
      2
      3
      4
      void Visit(BiTree T){			//访问结点
      	if(T->data!='#') 
      		cout<<T->data<<" ";
      }

      回到目录

    • 二叉树的递归遍历

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      oid PreOrder(BiTree T){			//递归先序遍历 
      	if(T!=NULL){
      		Visit(T);
      		PreOrder(T->lchild);
      		PreOrder(T->rchild);
      	}
      }

      void InOrder(BiTree T){			//递归中序遍历 
      	if(T!=NULL){
      		InOrder(T->lchild);
      		Visit(T);
      		InOrder(T->rchild);
      	}
      }

      void PostOrder(BiTree T){		//递归后序遍历 
      	if(T!=NULL){
      		PostOrder(T->lchild);
      		PostOrder(T->rchild);
      		Visit(T);
      	}
      }

    • 递归遍历改写为非递归

      递归代码看上去简单、简洁，但是其时间复杂度是呈指数型增长的，规模稍微一大，大家可想而知后果如何。所以一般以递归来分析问题，再改写为非递归形式。

    • 非递归先序遍历

      需要用到栈，前面已经实现过栈了，这里直接用库函数。

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      void PreOrder2(BiTree T){		//非递归先序遍历 
      	stack<BiTree> stack;
      	BiTree p=T;
      	while(p||!stack.empty()){
      	if(p!=NULL){
      		stack.push(p);
      		cout<<p->data<<" ";
      		p=p->lchild;
      	}
      	else{
      		p=stack.top();
      		stack.pop();
      		p=p->rchild;
      	}
        }
      }
    • 非递归中序遍历

      它与非递归先序遍历差不多，就是访问结点的时机不一样。 先序遍历在入栈过程中访问结点，后序遍历在出栈过程中访问结点。

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      void InOrder2(BiTree T){		//非递归中序遍历 
      	stack<BiTree> stack;
      	BiTree p=T;
      	while(p||!stack.empty()){
      	if(p!=NULL){
      		stack.push(p);
      		p=p->lchild;
      	}
      	else{
      		p=stack.top();
      		cout<<p->data<<" ";		
      		stack.pop();
      		p=p->rchild;
      	}
        }
      }
    • 非递归后序遍历

      这个是遍历中最难的，需要增加一个标记。
      和先序遍历、中序遍历非递归算法一样，后序遍历非递归算法同样是使用栈来实现：从根结点开始，将所有最左结点全部压栈，

    每当一个结点出栈时，要先扫描该结点的右子树， 只有当一个结点的左孩子和右孩子结点均被访问过了（标记 就可以看有没有访问了），才能访问结点自身。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    typedef struct BiTNodePost{
    	BiTree biTree;
    	char tag;
    }BiTNodePost,*BiTreePost;

    void PostOrder2(BiTree T){				//非递归后序遍历 
    	stack<BiTreePost> stack;
    	BiTree p=T;
    	BiTreePost BT;
    	while(p!=NULL||!stack.empty()){
    		while(p!=NULL){
    		BT=(BiTreePost)malloc(sizeof(BiTreePost));
    		BT->biTree=p;
    		BT->tag='L';
    		stack.push(BT);
    		p=p->lchild;
    	}
    	while(!stack.empty()&&(stack.top())->tag=='R'){
    		BT=stack.top();
    		stack.pop();
    		BT->biTree;
    		cout<<BT->biTree->data<<" ";
    	}
    	if(!stack.empty()){
    		BT=stack.top();
    		BT->tag='R';
    		p=BT->biTree;		
    		p=p->rchild;
    	}
      }
    }

    回到目录

    • 二叉树的层次遍历

      这里需要用到队列，前面已经实现过，这里直接用库函数。
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      void LevelOrder(BiTree T){				//层次遍历 
      	BiTree p=T;
      	queue<BiTree> queue;
      	queue.push(p);
      	while(!queue.empty()){
      		p=queue.front();
      		cout<<p->data<<" ";
      		queue.pop();
      		if(p->lchild!=NULL) queue.push(p->lchild);
      		if(p->rchild!=NULL) queue.push(p->rchild);
      	}
      }

    • 计算二叉树的深度

      1
      2
      3
      4
      5
      6
      7
      8
      9
      int Depth(BiTree T){				//二叉树的深度 
      	if(T==NULL) return 0;
      	else{
      		int m=Depth(T->lchild);
      		int n=Depth(T->rchild);
      		if(m>n) return m+1;
      		else return n+1;
      	}
      }

    • 计算二叉树的叶子节点个数

      1
      2
      3
      4
      int NodeCount(BiTree T){		//二叉树的叶子节点个数 
      	if(T==NULL) return 0;
      	else return NodeCount(T->lchild)+NodeCount(T->rchild)+1;
      }
      回到目录

    5.总的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
#include<iostream>
#include<stack>
#include<queue>
#include<stdlib.h> 
using namespace std;

typedef char datatype;

typedef struct BiTNode{			//二叉树节点 
	datatype data;
	struct BiTNode *lchild;
	struct BiTNode *rchild;
}BiTNode,*BiTree;

void init(BiTree &T){
	if((T=new BiTNode)!=NULL){
		T->data='A';
		T->lchild=NULL;
		T->rchild=NULL;
	}
	else{
		cout<<"初始化失败"<<endl;
		exit(1); 
	}
}

void CreateBiTree(BiTree &T){	//按先序序列创建二叉树 
	datatype data;
	cin>>data;
	if(data=='#') T=NULL;
	else {
		T=(BiTree)malloc(sizeof(BiTNode));
		T->data=data;
		CreateBiTree(T->lchild);
		CreateBiTree(T->rchild);
    }
}

void Visit(BiTree T){			//输出 
	if(T->data!='#') 
		cout<<T->data<<" ";
}

void PreOrder(BiTree T){//递归先序遍历 
	if(T!=NULL){
		Visit(T);
		PreOrder(T->lchild);
		PreOrder(T->rchild);
	}
}

void InOrder(BiTree T){//递归中序遍历 
	if(T!=NULL){
		InOrder(T->lchild);
		Visit(T);
		InOrder(T->rchild);
	}
}

void PostOrder(BiTree T){//递归后序遍历 
	if(T!=NULL){
		PostOrder(T->lchild);
		PostOrder(T->rchild);
		Visit(T);
	}
}

void PreOrder2(BiTree T){//非递归先序遍历 
	stack<BiTree> stack;
	BiTree p=T;
	while(p||!stack.empty()){
	if(p!=NULL){
		stack.push(p);
		cout<<p->data<<" ";
		p=p->lchild;
	}
	else{
		p=stack.top();
		stack.pop();
		p=p->rchild;
	}
  }
}

void InOrder2(BiTree T){//非递归中序遍历 
	stack<BiTree> stack;
	BiTree p=T;
	while(p||!stack.empty()){
	if(p!=NULL){
		stack.push(p);
		p=p->lchild;
	}
	else{
		p=stack.top();
		cout<<p->data<<" ";		
		stack.pop();
		p=p->rchild;
	}
  }
}

typedef struct BiTNodePost{
	BiTree biTree;
	char tag;
}BiTNodePost,*BiTreePost;

void PostOrder2(BiTree T){//非递归后序遍历 
	stack<BiTreePost> stack;
	BiTree p=T;
	BiTreePost BT;
	while(p!=NULL||!stack.empty()){
		while(p!=NULL){
		BT=(BiTreePost)malloc(sizeof(BiTreePost));
		BT->biTree=p;
		BT->tag='L';
		stack.push(BT);
		p=p->lchild;
	}
	while(!stack.empty()&&(stack.top())->tag=='R'){
		BT=stack.top();
		stack.pop();
		BT->biTree;
		cout<<BT->biTree->data<<" ";
	}
	if(!stack.empty()){
		BT=stack.top();
		BT->tag='R';
		p=BT->biTree;		
		p=p->rchild;
	}
  }
}

void LevelOrder(BiTree T){//层次遍历 
	BiTree p=T;
	queue<BiTree> queue;
	queue.push(p);
	while(!queue.empty()){
		p=queue.front();
		cout<<p->data<<" ";
		queue.pop();
		if(p->lchild!=NULL) queue.push(p->lchild);
		if(p->rchild!=NULL) queue.push(p->rchild);
	}
}

int Depth(BiTree T){			//二叉树的深度 
	if(T==NULL) return 0;
	else{
		int m=Depth(T->lchild);
		int n=Depth(T->rchild);
		if(m>n) return m+1;
		else return n+1;
	}
}

int NodeCount(BiTree T){		//二叉树的叶子节点个数 
	if(T==NULL) return 0;
	else return NodeCount(T->lchild)+NodeCount(T->rchild)+1;
}

int main(){
	BiTree T;
	init(T);
	cout<<"请输入一串字符构成二叉树"<<endl;
	CreateBiTree(T);
	cout<<"递归先序遍历"<<endl;
	PreOrder(T);
	cout<<endl;
	cout<<"非递归先序遍历"<<endl;
	PreOrder2(T);
	cout<<endl;
	cout<<"递归中序遍历"<<endl;
	InOrder(T);
	cout<<endl;
	cout<<"非递归中序遍历"<<endl;
	InOrder2(T);
	cout<<endl;
	cout<<"递归后序遍历"<<endl;
	PostOrder(T);
	cout<<endl;
	cout<<"非递归后序遍历"<<endl;
	PostOrder2(T);	
	cout<<endl;
	cout<<"层次遍历"<<endl;
	LevelOrder(T); 
	cout<<"二叉树的深度 ："<<Depth(T)<<endl;
	cout<<"二叉树的叶子节点个数 "<<NodeCount(T)<<endl;
	return 0;
}

6.运行结果：

在这里插入图片描述
回到目录

*[⌊i/2⌋]: 该符号表示不大于x的最大整数，即向下取整。

------------- Thank you for reading -------------
Title - Artist
0:00