哈弗曼树
定义:
假设有m个权值{w1,w2,…wm},可以构造一颗含n个叶子结点的二叉树,每个叶子结点的权重为wi,则其中带权路径长度WPL最小的二叉树称为最优二叉树或哈弗曼树。特点:
权值越大的结点离根节点越近。根据这个特点可以构造哈弗曼树。哈弗曼树的构造算法
根据给定的n个权值{w
1,w2,…wn},构造n棵只有根结点的二叉树。构成森林F。在森林F中选取两棵根结点权值最小的树作为左右子树构造一颗新的二叉树,置新二叉树根结点权值为其左右子树根节点权值之和。
从森林F中删除这两棵树,同时将新得到的二叉树加入森林F中。
重复(2)和(3),直到F只含一棵树为止,这棵树即是 哈弗曼树
演示过程:

回到目录哈弗曼算法的实现
哈弗曼的存储表示
1
2
3
4
5
6
7
8
9typedef struct {
char letter, *code; //letter字符,code生成的哈弗曼编码
int weight; //权重
int parent, lchild, rchild;
}HTNode, *HuffmanTree;构造哈弗曼树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89/*在HT[1...i]中选择parent为0且权值最小的结点
返回该结点的下标值
此函数被Select函数调用
*/
int Min(HuffmanTree &HT,int i) {
int j;
unsigned int k = UINT_iMAX; //假设各结点的权值不会超过UINT_MAX
int flag;
for(j = 1; j <= i; ++j){
if(HT[j].weight < k && HT[j].parent == 0){ //用父结点是否为0来判断此结点是否已经被选过
k = HT[j].weight; //找到最小值
flag = j;
}
}
HT[flag].parent = 1; //作个标记,说明已经被选择了。
return flag;
}
//在HT[1...i]中选择parent为0且权值最小的两个结点,其序号分别为s1,s2
//s1 <= s2
void Select(HuffmanTree &HT, int i, int &s1, int &s2) {
s1 = Min(HT,i);
s2 = Min(HT,i);
}
void CreateHuffmanTree(HuffmanTree &HT, char t[], int w[]){ //t[]为a[]形参,即字符,w[]为b[]形参,即权值
int m=2*n-1; //总共需要2n-1个节点
int i, s1, s2;
if(n<=1) //如果只有一个就不用创建
return ;
HT=new HTNode[m+1]; //开辟空间
for(i=1; i<=n; i++){ //将1-n号单元中的双亲、左孩子、右孩子的下标都初始化为0
HT[i].parent=0;
HT[i].lchild=0;
HT[i].rchild=0;
HT[i].code='\0';
HT[i].letter=t[i-1];
HT[i].weight=w[i-1];
}
for(i=n+1; i<=m; i++) { //初始化
HT[i].code='\0';
HT[i].parent=0;
HT[i].lchild=0;
HT[i].rchild=0;
HT[i].letter=' ';
HT[i].weight=0;
}
cout<<"-------------------------"<<endl; //初始化结束,以下开始创建哈夫曼树
for(i=n+1; i<=m; i++){
Select(HT, i-1,s1, s2); //在n个数中找出权值最小的两个
HT[s1].parent=i;
HT[s2].parent=i; //将他们两个的parent节点设置为i;
HT[i].lchild=s1;
HT[i].rchild=s2; //把这两个分别当作左右节点
HT[i].weight=HT[s1].weight+HT[s2].weight; //他们两个的双亲的权值为他们两个的和。
}
}
哈弗曼不等长编码
在构造哈弗曼树之后,求哈弗曼编码的思想是:
依次以叶子为出发点,向上回溯至根结点为止。回溯时走左分支则生成代码0,走右分支则生成代码1。
1 | void CreatHuffmanCode(HuffmanTree HT){ |
哈弗曼译码
1 | void HuffmanTreeYima(HuffmanTree HT,char cod[],int b) { //译码 |
总的代码:
1 | #include<iostream> |
运行结果:

上面运行结果存储变化:
HT的初态:
HT的终态: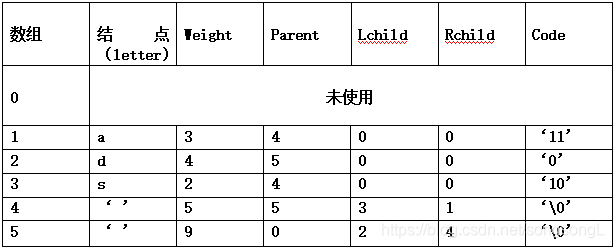
回到目录