最小生成树
在一个连通网的所有生成树中,各边的代价之和最小的那颗生成树称为该连通网的最小代价生成树,简称为最小生成树。
最小生成树主要有两种算法,普利姆(Prim)算法 && 克鲁斯卡尔(Kruskal)算法
普利姆(Prim)算法
普里姆算法在找最小生成树时,将顶点分为两个集合,一类是在查找的过程中已经包含在树中的顶点集U,另一类V(总-U)顶点集。
从U与V中找一条权值最小的边,同时将V中的顶点并入U中。
可以看出,普利姆(Prim)算法逐步增加U中的顶点,可称为加点法。辅助数组
1
2
3
4
5
6typedef struct{
vertexType adjvex; //最小边在U中的顶点
arcType lowcost; //最小边的权值
}ClosEdge;
ClosEdge closedge[MVNum];该辅助数组记录着集合U中到集合V中的最小权值边。
普利姆(Prim)算法
需要注意的是: V中的点并入了U中时,需要更新U到V的权值。更新后辅助数组中可能存着U中不同的顶点到V的距离。然后选择最小的作为最小生成树的。
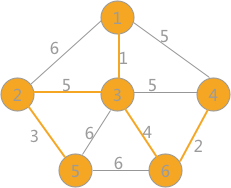
有点抽象,举个例子说明,结合着代码看:
该图以这样的邻接矩阵存着:**Z是一个足够大的值**

一开始:以V0为起点。closedge[ ]数组如下所示:

0是在集合U中的标志,找到最小权值1,对应的V集合中的顶点是下标2位置确定的顶点V3。当然V3与V1连接。
此时应该更新V3并入之后,closedge[ ]数组的变化。
两段划线的相比,取其小的更新closedge[ ]数组:
得到更新后的closedge[ ]数组:

找到最小权值4,对应的V集合中的顶点是下标5位置确定的顶点V6。当然V6与V3连接。
然后将V6并入U集合中,这样以此类推。。。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34int Prim(Graph g, vertexType u) { //分成两堆。U集合与V集合(总-U)
int weight=0; //累计最小生成树的权值
int i,j,k;
k=FindPos(g,u); //以u为起点,确定u的位置
for (i = 0; i < g->vexnum; i++) {
if(i!=k){
closedge[i]={u,g->Arc[k][i]}; //u顶点到,i位置确定的顶点,的权值,初始化为邻接表中对应的值
}
}
closedge[k].lowcost=0; // 初始时U集合只有u点,在U集合里,就记为0
for (j = 1; j < g->vexnum; j++) {
k=Min(g,closedge); //找到最小权值。当然也就知道顶点
vertexType u0 = closedge[k].adjvex; //最小边在U中的顶点
vertexType v0 = g->vertex[k]; //最小边在V中的顶点
printf("%c,%c\n",u0,v0);
weight=weight+g->Arc[FindPos(g,u0)][k]; //最小生成树的权值
closedge[k].lowcost=0; //将k确定的顶点放入集合U中
for (i = 0; i < g->vexnum; i++) { //由于k顶点加入U中,检查k到其他顶点的权值是否比k加入之前小
if (g->Arc[k][i] < closedge[i].lowcost) {
closedge[i] ={g->vertex[k],g->Arc[k][i]}; // 更新
}
}
}
return weight;
}具体代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153#include<iostream>
#include<stdlib.h>
using namespace std;
#define MVNum 10 //最大顶点数
#define MAXINT 32768 //表示极大值
typedef int arcType;
typedef char vertexType;
typedef struct MNode{
vertexType vertex[MVNum]; //存储顶点
arcType Arc[MVNum][MVNum]; //邻接矩阵,存储边
int vexnum,arcnum;
}GraphNode,*Graph;
int Init(Graph &G){
G=(GraphNode *)malloc(sizeof(GraphNode));
G->vexnum=0;
G->arcnum=0;
if(G) return 1;
else cout<<"初始化出错!"<<endl;
return 0;
}
int FindPos(Graph G,char a){//查找位置
int pos=-1;
for(int i=0;i<G->vexnum;i++){
if(G->vertex[i]==a){
pos=i;
}
}
return pos;
}
void CreateUDN(Graph G) //创建无向网
{
int num=0, //控制输入顶点数
pos1,pos2, //确认顶点位置
i,j,
weight; //权值
char a,
b,
ch; //顶点
for(i = 0;i<MVNum; i++){ //初始化弧
for(j = 0;j<MVNum; j++){
G->Arc[i][j] = MAXINT;
}
}
printf("请输入顶点(不超过10个,以#结束):\n");
cin>>ch;
while(ch!='#' && num <10){
G->vertex[num] = ch;
cin>>ch;
num++;
}
G->vexnum = num; //顶点个数
cout<<"请输入对应的弧(ab与ba是一样的边)和权值,以###结束"<<endl;
cin>>a>>b>>weight;
while(a!='#' && b!='#'){
cout<<a<<"-"<<b<<":"<<weight<<endl;
pos1=FindPos(G,a);
pos2=FindPos(G,b);
printf("位置a:%d,位置b:%d\n",pos1,pos2);
if(pos1!= -1 && pos2!= -1){ //忽略不存在的顶点
G->Arc[pos1][pos2] = weight;
G->Arc[pos2][pos1] = weight;
G->arcnum++;
}
cin>>a>>b>>weight;
}
}
void PrintGraph(Graph g) {
cout << "图的顶点为:" << endl;
for (int i = 0; i < g->vexnum; i++) {
cout << g->vertex[i] << " ";
}
cout << endl;
cout << "图的邻接矩阵为:" << endl;
for (int i = 0; i < g->vexnum; i++) {
for (int j = 0; j < g->vexnum; j++) {
printf("%10d ",g->Arc[i][j]);
}
cout << endl;
}
}
typedef struct{
vertexType adjvex; //最小边在U中的顶点
arcType lowcost; //最小边的权值
}ClosEdge;
ClosEdge closedge[MVNum];
int Min(Graph g,ClosEdge a[]){
int j=0;
int min=MAXINT;
for(int i=0;i<g->vexnum;i++){
if(a[i].lowcost!=0 && a[i].lowcost<min){
min=a[i].lowcost;
j=i;
}
}
return j;
}
int Prim(Graph g, vertexType u) { //分成两堆。U集合与V集合(总-U)
int weight=0; //累计最小生成树的权值
int i,j,k;
k=FindPos(g,u); //以u为起点,确定u的位置
for (i = 0; i < g->vexnum; i++) {
if(i!=k){
closedge[i]={u,g->Arc[k][i]}; //u顶点到,i位置确定的顶点,的权值,初始化为邻接表中对应的值
}
}
closedge[k].lowcost=0; // 初始时U集合只有u点,在U集合里,就记为0
for (j = 1; j < g->vexnum; j++) {
k=Min(g,closedge); //找到最小权值。当然也就知道顶点
vertexType u0 = closedge[k].adjvex; //最小边在U中的顶点
vertexType v0 = g->vertex[k]; //最小边在V中的顶点
printf("%c,%c\n",u0,v0);
weight=weight+g->Arc[FindPos(g,u0)][k]; //最小生成树的权值
closedge[k].lowcost=0; //将k确定的顶点放入集合U中
for (i = 0; i < g->vexnum; i++) { //由于k顶点加入U中,检查k到其他顶点的权值是否比k加入之前小
if (g->Arc[k][i] < closedge[i].lowcost) {
closedge[i] ={g->vertex[k],g->Arc[k][i]}; // 更新
}
}
}
return weight;
}
int main(){
Graph G = NULL;
Init(G);
CreateUDN(G);
PrintGraph(G);
cout<<"权值"<<Prim(G,'1')<<endl;
return 0;
}运行结果:
克鲁斯卡尔(Kruskal)算法
克鲁斯卡尔(Kruskal)算法在找最小生成树时,先将边按权值大小排好序,在直接去拿最小的权值边,只需保证拿来的边不能产生回路即可。当拿了(n-1)条边且没有回路,就能构成最小生成树。
可以看出,克鲁斯卡尔(Kruskal)算法逐步增加生成树的边,可称为加边法。而保证拿来的边不能产生回路,需要一个辅助数组,初始时,数组里存着每个顶点不同的标记,即n个连通分量。当拿来一条边,看看这条边依附的两个顶点的标记相不相等,如果等,则说明在一个连通分量里,即会产生回路。不相等,则能构成最小生成树的边。
克鲁斯卡尔(Kruskal)算法
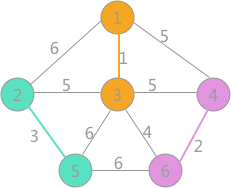
当确定了一条边时,需要将v2顶点及其与v2标记一样的顶点的标记改为v1的标记,因为他们在一个连通分量里。
还是上面那个网,当克鲁斯卡尔(Kruskal)算法选到这一步时,即将选择顶点3和6,不仅6要改为3的标记,4也要改为3的标记。所以需要用循环判断去改变标记。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32int Kruskal(Graph G) //最小生成树,克鲁斯卡尔算法
{
int i,j;
int V1,V2;
int vs1,vs2;
int weight=0; //累计最小生成树权值
Sort(G,G->edges);
for (i = 0; i < G->vexnum; i++){
Vexset[i] = i;
}
for (i = 0; i < G->arcnum; i++)
{
V1 = FindPos(G, G->edges[i].initial);
V2 = FindPos(G, G->edges[i].end);
vs1=Vexset[V1];
vs2=Vexset[V2];
if (vs1 != vs2) //若相等,说明有环
{
weight= weight+ G->edges[i].weight; //累计最小生成树权值
printf("(%c,%c):%d\n", G->edges[i].initial, G->edges[i].end, G->edges[i].weight);//打印边和权值
for(j=0;j<G->vexnum;j++){ //之所以要循环,就是因为有时(边变多时),要改变标记的点不止一个。
if(Vexset[j]==vs2){
Vexset[j]=vs1;
}
}
}
}
return weight;
}具体代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137#include<iostream>
#include<stdlib.h>
using namespace std;
#define MVNum 10 //最大顶点数
typedef int arcType;
typedef char vertexType;
typedef struct edge{
vertexType initial; //类似邻接矩阵横坐标
vertexType end; //类似邻接矩阵纵坐标
arcType weight; //权值
}Edge;
typedef struct MNode{
vertexType vertex[MVNum]; //存储顶点
Edge edges[MVNum]; //类似邻接矩阵
int vexnum,arcnum;
}GraphNode,*Graph;
int Vexset[MVNum];
int Init(Graph &G){
G=(GraphNode *)malloc(sizeof(GraphNode));
G->vexnum=0;
G->arcnum=0;
if(G) return 1;
else cout<<"初始化出错!"<<endl;
return 0;
}
int FindPos(Graph G,char a){//查找位置
int pos=-1;
for(int i=0;i<G->vexnum;i++){
if(G->vertex[i]==a){
pos=i;
}
}
return pos;
}
void CreateUDN(Graph G) //创建无向网
{
int num=0, //控制输入顶点数
pos1,pos2, //确认顶点位置
weight; //权值
char ch; //顶点
Edge e; //边
printf("请输入顶点(不超过10个,以#结束):\n");
cin>>ch;
while(ch!='#' && num <10){
G->vertex[num] = ch;
cin>>ch;
num++;
}
G->vexnum = num; //顶点个数
cout<<"请输入对应的弧(ab与ba是一样的边)和权值,以###结束"<<endl;
cin>>e.initial>>e.end>>e.weight;
int k=0;
while(e.initial!='#' && e.initial!='#'){
cout<<e.initial<<"-"<<e.end<<":"<<e.weight<<endl;
G->arcnum++;
G->edges[k] = e;
cin>>e.initial>>e.end>>e.weight;
k++;
}
}
void PrintGraph(Graph g) {
cout << "图的顶点为:" << endl;
for (int i = 0; i < g->vexnum; i++) {
cout << g->vertex[i] << " ";
}
cout << endl;
cout << "图的边为:" << endl;
for (int j = 0; j < g->arcnum; j++) {
printf("起点%c,终点%c,权值%8d\n",g->edges[j].initial,g->edges[j].end,g->edges[j].weight);
}
}
void Sort(Graph g,Edge a[]){
Edge temp;
for(int i=1;i<g->arcnum;i++){
for(int j=0;j<g->arcnum-i;j++){
if(a[j].weight>a[j+1].weight){
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
}
int Kruskal(Graph G) //最小生成树,克鲁斯卡尔算法
{
int i,j;
int V1,V2;
int vs1,vs2;
int weight=0; //累计最小生成树权值
Sort(G,G->edges);
for (i = 0; i < G->vexnum; i++){
Vexset[i] = i;
}
for (i = 0; i < G->arcnum; i++)
{
V1 = FindPos(G, G->edges[i].initial);
V2 = FindPos(G, G->edges[i].end);
vs1=Vexset[V1];
vs2=Vexset[V2];
if (vs1 != vs2) //若相等,说明有环
{
weight= weight+ G->edges[i].weight; //累计最小生成树权值
printf("(%c,%c):%d\n", G->edges[i].initial, G->edges[i].end, G->edges[i].weight);//打印边和权值
for(j=0;j<G->vexnum;j++){ //之所以要循环,就是因为有时(边变多时),要改变标记的点不止一个。
if(Vexset[j]==vs2){
Vexset[j]=vs1;
}
}
}
}
return weight;
}
int main()
{
Graph G = NULL;
Init(G);
CreateUDN(G);
PrintGraph(G);
cout<<"最小生成树权值"<<Kruskal(G);
return 0;
}运行结果:
图的应用--最小生成树
-------------
Thank you for reading
-------------