songsong的垃圾堆

收废铜烂铁~

0%

二叉排序树

发表于 更新于 阅读： Valine：
本文字数： 2.1k 阅读时长 ≈ 8 分钟

二叉排序树的定义

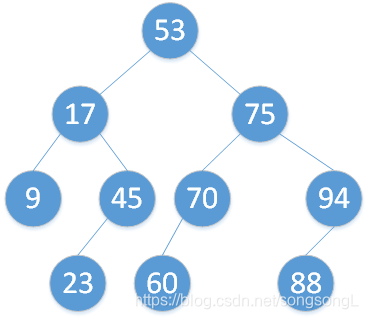
二叉排序树，又叫二叉查找树，如果非空，则具有以下性质：

  1. 若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
  2. 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
  3. 它的左右子树也分别为二叉排序树。

由定义可得出 二叉排序树的一个重要性质： 中序遍历该二叉树可以得到一个结点值递增的有序序列。

结点定义

1
2
3
4
5
6
7
8
9
10
11
12
13
   //----------二叉排序树存储表示-----------
typedef struct{						
	KeyType key;										//关键字项 
	OtherInfo info;										//其他数据信息 
													
}ElemType;

typedef struct BSTNode {
	ElemType data;									//每个结点的数据域包括关键字项和其他信息 
	struct BSTNode *lchild;
	struct BSTNode *rchild;							    
	                                                                                                                                                                                                                                                                
} BSTNode,*BSTree;

二叉排序树的操作

  • 查找

    • 若key == T->data.key，则查找成功，返回根节点地址。
    • 若key < T->data.key，则进一步查找左子树。
    • 若key > T->data.key，则进一步查找右子树。
      1
      2
      3
      4
      5
      6
      7
      BSTree SearchBST(BSTree T,KeyType key) {
       	if ((!T)|| key == T->data.key)
              return T;
          else if (key < T->data.key)
              return SearchBST(T->lchild, key);
          else return SearchBST(T->rchild, key);
      }
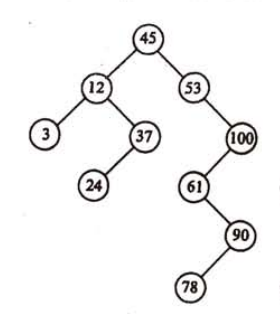
      在这里插入图片描述
      要找100，与45比较，大于，然后与53比较，大于，与100比较，找到。
      在二叉排序树上查找关键字等于给定的值的结点过程，恰是走了一条从根结点到该结点路径的过程。因此和折半查找类似，与给定值比较的关键字个数不超过树的深度。

  • 插入

    二叉排序树的插入操作是以查找为基础的。当树中不存在关键字等于key的结点时才插入。新插入的结点一定是一个新添加的叶子结点，并且是查找不成功时查找路径上访问的最后一个结点的左孩子或右孩子结点。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    void InsertBST(BSTree &T,ElemType e)
    {
    	if(!T){										//找到插入位置 
    		BSTree S=new BSTNode;					//新节点保存数据 
    		S->data=e;
    		S->lchild=S->rchild=NULL;
    		T=S;									//把新结点放到已找到的插入位置 
    	}
        else if(e.key < T->data.key) 
    		InsertBST(T->lchild,e); 
      	else if(e.key > T->data.key) 
      		InsertBST(T->rchild,e); 
      	else{
      		cout<<"已有此值~"<<endl;
      		return;
    	}
    }

    • 创建

      从空开始，每输入一个结点，经过查找，插入到二叉排序树的合适位置。
      一个无序序列可以通过构造一棵二叉排序树而变成一个有序序列，构造树的过程即为对无序序列进行排序的过程。 
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      void CreateBST(BSTree &T) {					
      			
      	T=NULL;
      	ElemType e; 
      	cout << "请输入值：0结束"<<endl;			
      	cin >> e.key;
      	
      	while (e.key!=0) {
      		InsertBST(T,e);	
      		cout << "请继续输入"<<endl;		
      		cin>>e.key;	
      	}
      }

返回顶部

  • 删除

    删除节点的情况相对复杂，主要分为以下三种情形：

      1. 被删除的结点是叶子
  2. 被删除的结点只有左子树或者只有右子树
  3. 被删除的结点既有左子树，也有右子树

    第1、2种比较简单，主要说一下第3种。
    删除结点有两种策略：以删除78为例,下面用到的s都是中序遍历时待删除结点的直接前驱。 二叉树的操作移步hear。

    第一种：

    1
    2
    s->rchild = p->rchild;
    p = p->lchild;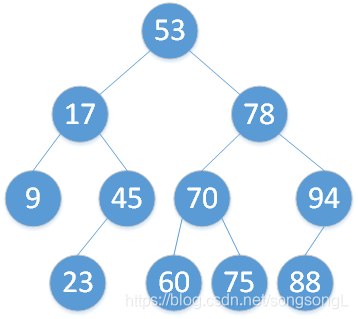

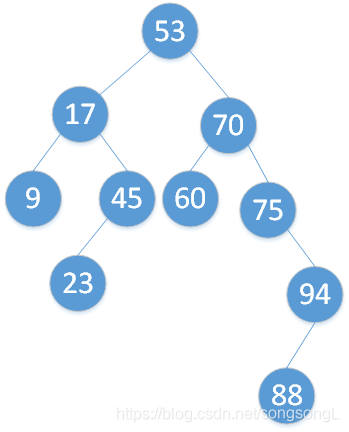
    在这里插入图片描述
    在这里插入图片描述

从图可以看出这种方法会增加树的深度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void delete_Node1(BSTree &p)	
{ 
	BSTree q,s;
	if(!p->lchild)	//由于这个if在前面，所以左右子树均为空的情况会在这里处理 
	{	//如果左子树为空，则只需重接其右子树
		q = p;
		p = p->rchild ;
		free(q);
	}
	else if(!p->rchild)
	{	//如果右子树为空，则只需重接其左子树
		q = p;
		p = p->lchild;
		free(q);
	}
	else
	{	//如果左右子树都不为空，这里采取修改左子树的方法，也可以修改右子树，方法类似
		s = p->lchild;		//取待删节点的左孩子结点
 
		while(s->rchild)	//找到中序遍历时会得到的直接前驱 
			s = s->rchild;
		s->rchild = p->rchild;	//将p的右子树接为s的右子树
		q = p;
		p = p->lchild;		//将p的左子树直接接到其父节点的左子树上
		free(q);
	}
}

第二种：用s替代待删除结点。
1
p->data = s->data;

在这里插入图片描述
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
void delete_Node2(BSTree &p)
{
	BSTree q,s;		
	if(!p->lchild)		//由于这个if在前面，所以左右子树均为空的情况会在这里处理 
	{	//如果左子树为空，则只需重接其右子树
		q = p;
		p = p->rchild ;
		free(q);
	}
	else if(!p->rchild)
	{	//如果右子树为空，则只需重接其左子树
		q = p;
		p = p->lchild;
		free(q);
	}
	else
	{	//如果左右子树都不为空，采取修改左子树的方法，也可以修改右子树，方法类似
		q = p;
		s = p->lchild;		//取待删节点的左节点
		while(s->rchild)		
		{		//找到中序遍历时会得到的直接前驱 
			q = s;
			s = s->rchild;
		}
		//用s来替换待删节点p
		p->data = s->data;  
		//根据情况，将s的左子树重接到q上
		if(p != q)
			q->rchild = s->lchild;
		else
			q->lchild =s->lchild;
		free(s);
	}
}

返回顶部

总的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
#include <iostream>
#include<stdlib.h>
using namespace std;

typedef int KeyType;
typedef int OtherInfo;

   //----------二叉排序树存储表示-----------
typedef struct{						
	KeyType key;										//关键字项 
	OtherInfo info;										//其他数据信息 
													
}ElemType;

typedef struct BSTNode {
	ElemType data;									//每个结点的数据域包括关键字项和其他信息 
	struct BSTNode *lchild;
	struct BSTNode *rchild;							    
	                                                                                                                                                                                                                                                                
} BSTNode,*BSTree;

void PreOrder(BSTree T){//递归先序遍历 
	if(T!=NULL){
		cout<<T->data.key<<" ";
		PreOrder(T->lchild);
		PreOrder(T->rchild);
	}
}

void InOrder(BSTree T){//递归中序遍历 
	if(T!=NULL){
		InOrder(T->lchild);
		cout<<T->data.key<<" ";
		InOrder(T->rchild);
	}
}

BSTree SearchBST(BSTree T,KeyType key) {
 	if ((!T) || key == T->data.key)
        return T;
    else if (key < T->data.key)
        return SearchBST(T->lchild, key);
    else return SearchBST(T->rchild, key);
}

void InsertBST(BSTree &T,ElemType e)
{
	if(!T){										//找到插入位置 
		BSTree S=new BSTNode;					//新节点保存数据 
		S->data=e;
		S->lchild=S->rchild=NULL;
		T=S;									//把新结点放到已找到的插入位置 
	}
    else if(e.key < T->data.key) 
		InsertBST(T->lchild,e); 
  	else if(e.key > T->data.key) 
  		InsertBST(T->rchild,e); 
  	else{
  		cout<<"已有此值~"<<endl;
  		return;
	}
}

void delete_Node1(BSTree &p)	
{ 
	BSTree q,s;
	if(!p->lchild)	//由于这个if在前面，所以左右子树均为空的情况会在这里处理 
	{	//如果左子树为空，则只需重接其右子树
		q = p;
		p = p->rchild ;
		free(q);
	}
	else if(!p->rchild)
	{	//如果右子树为空，则只需重接其左子树
		q = p;
		p = p->lchild;
		free(q);
	}
	else
	{	//如果左右子树都不为空，这里采取修改左子树的方法，也可以修改右子树，方法类似
		s = p->lchild;		//取待删节点的左孩子结点
 
		while(s->rchild)	//找到中序遍历时会得到的直接前驱 
			s = s->rchild;
		s->rchild = p->rchild;	//将p的右子树接为s的右子树
		q = p;
		p = p->lchild;		//将p的左子树直接接到其父节点的左子树上
		free(q);
	}
}
 
void delete_Node2(BSTree &p)
{
	BSTree q,s;		
	if(!p->lchild)		//由于这个if在前面，所以左右子树均为空的情况会在这里处理 
	{	//如果左子树为空，则只需重接其右子树
		q = p;
		p = p->rchild ;
		free(q);
	}
	else if(!p->rchild)
	{	//如果右子树为空，则只需重接其左子树
		q = p;
		p = p->lchild;
		free(q);
	}
	else
	{	//如果左右子树都不为空，采取修改左子树的方法，也可以修改右子树，方法类似
		q = p;
		s = p->lchild;		//取待删节点的左节点
		while(s->rchild)		
		{		//找到中序遍历时会得到的直接前驱 
			q = s;
			s = s->rchild;
		}
		//用s来替换待删节点p
		p->data = s->data;  
		//根据情况，将s的左子树重接到q上
		if(p != q)
			q->rchild = s->lchild;
		else
			q->lchild =s->lchild;
		free(s);
	}
}

bool delete_BSTree(BSTree &T,int key)
{
	//不存在关键字为key的节点
	if(!T)
		return false;
	else
	{	
		if(SearchBST(T,key))      //查找到关键字为key的节点
		{
			//delete_Node1(T);
			delete_Node2(T);
			return true;			
		}
		else  
		{
			cout<<"查无此值~"<<endl; 
			return false;			
		}                 
	}
}

void CreateBST(BSTree &T) {					
			
	T=NULL;
	ElemType e; 
	cout << "请输入值：0结束"<<endl;			
	cin >> e.key;
	
	while (e.key!=0) {
		InsertBST(T,e);	
		cout << "请继续输入"<<endl;		
		cin>>e.key;	
	}
}

void destroy_BSTree(BSTree pTree)	//递归销毁二叉排序树
{
	if(pTree)
	{
		if(pTree->lchild)
			destroy_BSTree(pTree->lchild);
		if(pTree->rchild)
			destroy_BSTree(pTree->rchild);
		free(pTree);
		pTree = NULL;
	}
}

int main(){
	BSTree T;
	CreateBST(T);
	cout<<"删除前"<<endl;
	cout<<"先序遍历:";
	PreOrder(T); 
	cout<<endl<<"中序遍历:";
	InOrder(T);
	cout<<"请输入删除的关键字"<<endl;
	int i;
	cin>>i;				
	while (i!=0) {
		delete_BSTree(T,i);
		InOrder(T);
		cout << "请继续输入"<<endl;		
		cin>>i;	
	}
	cout<<"删除后"<<endl;
	InOrder(T);
	return 0;
}

运行结果：

在这里插入图片描述
在这里插入图片描述
返回顶部

------------- Thank you for reading -------------
Title - Artist
0:00